Las industrias de la logística, las materias primas y muchas otras dependen en buena medida de los métodos de optimización que proporcionan las matemáticas. En particular los algoritmos de empaquetamiento son especialmente importantes. Aparecen en escena cuando hay que encontrar la forma óptima de empaquetar más objetos en una caja, en el transporte de contenedores o al cortar piezas de telas u otros materiales formas diversas para aprovecharlo al máximo.
Estos problemas reales, que van desde cómo meter más naranjas en una caja a cómo organizar un «tetris» de paquetes de distintas formas o pesos, pueden idealizarse de muchas formas. A lo largo de la historia los matemáticos han inventado métodos muy eficaces, pero también han descubierto que a veces esto se convierte en un problema computacional complejo –cuya dificultad aumenta exponencialmente con el número de objetos o de restricciones planteadas– y sólo se puede aspirar a una solución aproximada, aunque sea al 99%. Veamos algunos casos típicos.
El problema de la mochila consiste en encontrar la forma óptima de meter en una mochila una varios objetos de una lista, cada uno de los cuales tiene un «valor» y un peso determinados. La restricción es que no pueden pesar de lo que se define de antemano. El objetivo es que el «valor total» sea máximo. Por ejemplo estos objetos podrían ser A, B, C y D con valores 3, 9, 12 y 8 y pesos 1, 3, 4 y 2. Si el peso máximo de la mochila se limita a 5 la solución es empaquetar A+C = valor 15, peso 5. Otra soluciones valen menos o pesan más de 5 y no son válidas.
Hay diversas formas de solucionar este problema: una de ellas es probar todas las combinaciones (búsqueda exhaustiva), pero éstas aumentan exponencialmente cuantos más objetos hay o más restricciones se aplican. Otra es utilizar la llamada programación dinámica, que aun así puede ser lenta en encontrar una solución para muchos objetos. Otra más es por aproximación: en muchos casos hay formas de encontrar una solución cercana al valor que se consideraría óptimo. El problema de la mochila es un problema teórico muy interesante porque otros similares se pueden reducir a este; por ejemplo, cómo recortar tela o metal en piezas de ciertos tamaños. En la práctica los ordenadores más potentes y la programación dinámica resuelven el problema incluso para un gran número de objetos.
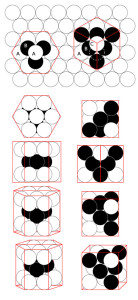El empaquetamiento de objetos regulares. Si todos los objetos formaran patrones regulares que rellenaran el plano o el espacio –y además pudiéramos fabricar las cajas a medida– todo esto sería más fácil. Pero por ejemplo las naranjas y otros objetos esféricos han traído de cabeza a los matemáticos durante siglos. De hecho se suele decir que los fruteros y los soldados que apilaban balas de cañón lo resolvieron «en la práctica» mediante ensayo y error. Estudiando el empaquetamiento de esferas los matemáticos descubrieron que las esferas apiladas al azar suelen ocupar cualquier espacio con una densidad del ~64%. Pero si se disponen cuidadosamente en capas –hay al menos tres formas de hacerlo– se puede llegar al 74%, que es bastante más.
Más allá de las naranjas los matemáticos han examinado con bastante éxito la forma óptima de empaquetar conjuntos de esferas de dos tamaños distintos, o incluso de otros poliedros, algo que tiene su aplicación en química por la forma en que se disponen los cristales de algunos materiales.
Una curiosidad del empaquetamiento aleatorio de algunos productos (ej. los granos irregulares en un tarro o saco) es que pueden ocupar un volumen inicial cuando se meten en el recipiente y luego sufrir una redistribución más densa al ser agitados. Por eso en algunos envases industriales se indica que «el volumen puede variar durante el transporte», para que nadie se crea que hay menos producto cuando llega que cuando sale del lugar de origen. El peso es el mismo: sólo varía que está más densamente empaquetado debido a la gravedad y el movimiento.
Algunos otros problemas matemáticos de empaquetamiento de tipo práctico incluyen las formas óptimas de empaquetar círculos dentro de un círculo (y que sea lo más pequeño posible), donde el máximo que se conoce son 13 círculos con densidad 72,4%; los círculos en un cuadrado, con un caso notable de 15 círculos en un cuadrado de lado 7,86 veces el radio de los círculos o incluso cuadrados en un cuadrado, con el curioso caso de los 10 cuadrados en un cuadrado de lado 3,7 veces el lado de los cuadrados. Es divertido intentar igualar esto «a mano».
Si alguien se pregunta por qué todo esto es importante sólo tiene que hacer números. Por poner un ejemplo, los expertos en optimización de Isazi Consulting cuentan de un caso en el que en un puerto consiguieron meter en 29 contenedores TEU los mismos palés que originalmente requerían 30 contenedores. El cliente exportaba 300 contenedores al mes, de modo que comenzó a ahorrarse 10 al mes. Al final del año el coste de transportar 120 contenedores menos resultó ser un buen ahorro, especialmente para el bolsillo. Y todo gracias al uso de las matemáticas.
_____
{Foto (CC) Curology @ Unsplash; Spheres (PD) Wikipedia; Knapsack (CC) Wikimedia}
Nos encantará conocer tu opinión, pero primero tenemos que indicarte que los comentarios están moderados, y no aparecerán inmediatamente en la página al ser enviados. Evita, por favor, las descalificaciones personales, los comentarios maleducados, los ataques directos o ridiculizaciones personales, o los calificativos insultantes de cualquier tipo, sean dirigidos a los autores, a cualquier otro comentarista o la empresa propietaria de esta página. Estás en tu perfecto derecho de comentar anónimamente, pero por favor, no utilices el anonimato para decirles a las personas cosas que no les dirías en caso de tenerlas delante. Intenta mantener un ambiente agradable en el que las personas puedan comentar sin temor a sentirse insultados o descalificados. No comentes de manera repetitiva sobre un mismo tema, y mucho menos con varias identidades o suplantando a otros comentaristas. También, procura que tus opiniones estén relacionadas con lo que se comenta en esta entrada. Los comentarios off-topic, promocionales, o que incumplan todas estas normas básicas serán eliminados.