Cualquiera que haya tenido que preparar una caja para un envío con muchos pequeños objetos, llenado el maletero del coche para salir en vacaciones o intentado aprovechar una furgoneta en una mudanza sabe lo complejo que resulta optimizar el empaquetamiento en tres dimensiones. Lo mismo le ocurre a los interiores de los dispositivos electrónicos, ordenadores y al interior de los coches, donde cientos de piezas compiten por cada milímetro cúbico. Esto se conoce matemáticamente como problemas de empaquetado 3D y es algo tremendamente complejo, especialmente cuando los objetos no son todos iguales, como sucede generalmente.
Ahora un equipo del Instituto de Tecnología de Massachusetts y de la empresa Inkbit ha desarrollado un nuevo algoritmo, llamado Empaquetamiento Espectral Denso [PDF] que funciona sorprendentemente bien. No es algo al alcance de los cálculos humanos, pero para los ordenadores actuales no supone un problema.
El empaquetamiento, un reto matemático
Dado que el empaquetamiento de objetos afecta a muchos campos de la sociedad y los negocios, es normal que se haya tratado desde tiempos inmemoriales. Además de las soluciones obvias de la antigüedad, en el siglo XVII y XVIII, Newton y Leibnz desarrollaron las herramientas geométricas y de cálculo que provenían de los tiempos de Euclides para abordar el problema. Kepler fue uno de los que trabajó en muchas de sus variantes, entre ellas el empaquetamiento de esferas como caso sencillo y típico. Lo que se busca es la forma de colocar un mayor número de esferas en el menor volumen posible. La solución básica la conocían bien los fruteros o los soldados que apilaban naranjas o balas de cañón: una estructura piramidal. Pero si la base o el contenedor son distintos, como en el caso de bases triangulares o hexagonales, o es un espacio abierto, como sucede en los minerales, la solución puede ser distinta.
Con la llegada de los ordenadores del siglo XX, estos problemas se pudieron resolver con métodos como «fuerza bruta», «mejor encaje», «primer encaje», «algoritmos genéticos» y otras técnicas. La capacidad de cómputo permitía encontrar soluciones que no eran las ideales pero se acercaban mucho a las óptimas. En la práctica esto era más que suficiente, especialmente en algo tan complicado como es el empaquetamiento en 3D.
En el siglo XXI han surgido nuevas ideas mucho más potentes, que unidas a la capacidad de cálculo multiplicada miles de veces ha hecho que resolver el problema sea cuestión de segundos. Hay algoritmos mucho más avanzados capaces que pueden probar las orientaciones de todos los objetos a empaquetar, que además pueden ser totalmente distintos. También pueden hacer los cálculos evitando que se queden encajados, o teniendo en cuenta los materiales de que están fabricados (y si son flexibles, delicados o no) y detalles similares. Lo más parecido al mundo real que se puede imaginar.
Empaquetar el tetris más complicado del mundo
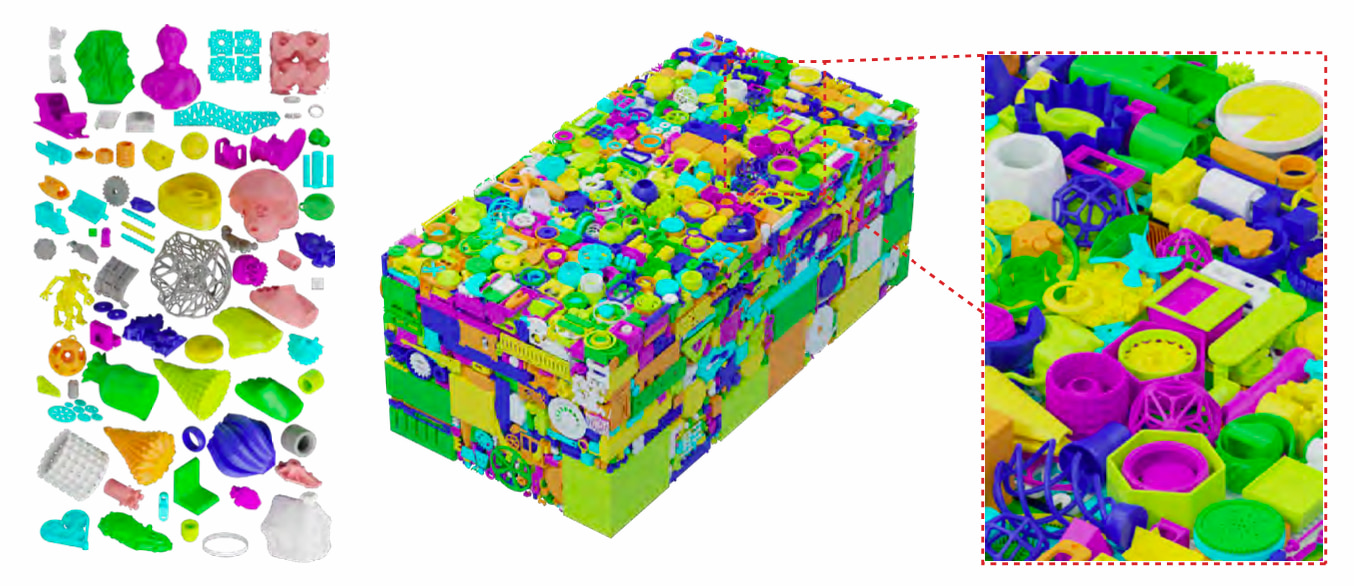
¿Cómo funciona el nuevo algoritmo? Básicamente sigue tres pasos bien definidos, con la ventaja de que puede aplicarse no solo a unas pocas decenas o cientos de objetos, sino a miles de ellos:
- Paso 1. Buscar posibles ubicaciones para cada objeto. Cada objeto se digitaliza y se convierte en vóxeles, que son como píxeles cúbicos en 3D (típicamente un vóxel tiene 1 ó 2 mm de lado). Pasan a estar representados digitalmente como las piezas pixeladas del Tetris, pero en tres dimensiones. Esto permite moverlos en el interior del contenedor y calcular rápidamente si hay colisiones con otros objetos o no.
- Paso 2. Detección de objetos encajados y corrección. Los objetos tienen que poder apilarse y moverse libremente. Si por su forma unos quedan encajados con otros (imaginemos dos rosquillas enlazadas, o las patas de una mesa), esa solución no sirve y hay que corregirla o descartarla.
- Paso 3. Optimización. Este último paso busca aproximarse lo más posible al objetivo, que se define como «lograr la mayor densidad de empaquetamiento». La densidad se calcula dividiendo el volumen que ocupan los objetos entre el volumen del contenedor. A medida que se colocan los objetos se priorizan los valores más altos (están «mejor colocados») pero se puede retroceder si el valor baja al colocar otros más adelante (pues estarían «mal colocados»). La idea es que las soluciones de cada zona del contenedor sea óptima, con la esperanza de que la solución final también lo sea.
Si suena complicado es porque lo es
¿Cómo se sabe si este algoritmo funciona correctamente? Sus creadores utilizaron un conjunto de datos de 6.000 objetos 3D que están disponibles en Thingi10K para quienes se dedican a la investigación. Lo probaron en un contenedor con forma de paralelepípedo con vóxeles de 1 y 2 mm, con tamaños como 480x245x200mm y 1430x730x597mm. También usaron una impresora 3D para imprimir pacientemente las piezas en plástico y comprobar algunas soluciones. Comparándolo con otros algoritmos obtuvieron densidades de empaquetamiento casi óptimas en tiempos razonables de unos segundos o unos pocos minutos.
Aunque toda esta explicación de cómo funciona el algoritmo suena complicada, basta imaginarlo como una caja negra capaz de tomar una lista de piezas, ya sean cajas, piezas de un reloj o componentes un teléfono móvil o muebles de una mudanza y proporcionar una solución razonable en unos pocos segundos.
Entre las aplicaciones potenciales están el campo de la robótica y la automatización, la optimización de espacio y costes en los envíos y la fabricación de todo tipo de dispositivos con componentes más compactos y miniaturizados. Y si bien los humanos pueden encontrar complicado organizar los paquetes u objetos en las posiciones adecuadas, para eso están los robots, esos incansables ayudantes capaces de interpretar estas soluciones colaborando en colocar todo en cuestión de segundos.
Nos encantará conocer tu opinión, pero primero tenemos que indicarte que los comentarios están moderados, y no aparecerán inmediatamente en la página al ser enviados. Evita, por favor, las descalificaciones personales, los comentarios maleducados, los ataques directos o ridiculizaciones personales, o los calificativos insultantes de cualquier tipo, sean dirigidos a los autores, a cualquier otro comentarista o la empresa propietaria de esta página. Estás en tu perfecto derecho de comentar anónimamente, pero por favor, no utilices el anonimato para decirles a las personas cosas que no les dirías en caso de tenerlas delante. Intenta mantener un ambiente agradable en el que las personas puedan comentar sin temor a sentirse insultados o descalificados. No comentes de manera repetitiva sobre un mismo tema, y mucho menos con varias identidades o suplantando a otros comentaristas. También, procura que tus opiniones estén relacionadas con lo que se comenta en esta entrada. Los comentarios off-topic, promocionales, o que incumplan todas estas normas básicas serán eliminados.